前回ボールの投げ上げの初速を計算したり、その初速で角度を変えた時の飛距離を計算してみました。ただ結局のところ式2つを自動的に計算するものでした。
いや、その式の自動化だけでも結構便利なんですけどね。
ただ、一瞬で計算結果が出るので(普通の利用ではそれで良いのですが)ちょっと頑張ってもらおうかなということで、ループを使った計算をしてみたいなと思った次第です。
弾道計算で目標に命中させる
前回のボール投げと似た形で、大砲の弾を目標に命中させる角度を求めてみることを考えてみます。初速が与えられた状態である距離にある目標へ着弾させるには、砲身の角度を何度にして打てばよいか?
を考えてみます。
初速は大砲の装薬量によってあらかじめ知っておくものとします。先のボール投げのように観測射撃をして初速を出しても良いでしょう。
前回のlの式を使います。
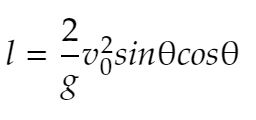
角度を知りたいので、θの式にすればよいのですね
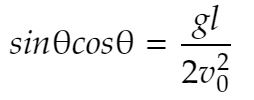
両辺が一致する時のθが目標角度。
右辺は決まっているので、θを0度~45度まで探索していきます。
?→A:?→B:4.9×B÷A^2→C▲0→D:0→M:Lbl0:D+.1→D:D≧45⇒Goto1:sinDcosD→M:C>M⇒Goto0:Lbl1:D▲
A:初速、B:目標距離 を入力すると、0.1度ごとに到達距離を計算して目標距離以上になったらループから抜けてその時の角度を出します。答えが45.1度になるとその速度では到達不能となります。
0度から角度を上げていますが、45度からやれば到達しない場合は一瞬でわかるのでそっちのほうが良いかも。
効率化?
また、N度ずつ上げていき、超えたらN度戻して探索角度を×0.1倍にしていって必要精度まで上げるということをやれば計算量は減りますね。
?→A:?→B:4.9×B×÷A^2→C▲-5→X:10→D:0→Y:Lbl0:Y+1→Y:X+D→X:D>50⇒Goto1:sinXcosX→M:C>M⇒Goto0:.001≧D⇒Goto1:X-D→X:D×.1→D:Goto0:Lbl1:X▲
もう36Step程度のプログラム関数電卓では入りきらないです。
・A(初速)を入力
・ B(目標距離)を入力
・ 右辺を計算してメモリーCへ
・ 初期角度を-5度に(計算角度はXを利用)
・ 探索粒度を10に(探索粒度はDを利用)
・ ループ量初期化(Y)
・ ラベル0
・ ループ量+1
・ X+D→X(計算角度を上げる)
・ 角度が50度を超えていたら終了(届かない)
・ sinXcosXを計算してMメモリー
・ CとMを比較して超えていなければラベル0へループ
・(CとMの比較が超えていたら)
・現在の探索粒度が設定値(0.001度)なら終了
・(探索粒度が設定値でなければ)
・X-D→Xで一つ前に戻す
・粒度を1桁上げる(D×0.1→D)
・ラベル0に飛ぶ
・ラベル1
・求めた角度Xを表示して終了
これなら0.1度ずつ探さなくてもいいですね。-5度からやっているのは10度粒度でも45度の計算をしないと困るから。
例えば答えが27.12°だった場合、5°→15°→25°→35°(ここで超えるので1つ戻して粒度を下げる以下同じ)→25°→26°→27°→ 28° (粒度下) →27.0°→27.1° →27.2° (粒度下)→27.10° →27.11° →27.12° →27.13° (粒度下)→27.120° →27.121°(終わり) となります。 ちなみにメモリーYに何回計算したかカウントしています。メモリーが足りなければ削れる所です。
というか効率的な計算方法を探しているのではなくて、ループの計算をさせて負荷をかけたいので効率の良いやりかたとかはまた後ですかね。実用っぽいことを題材に計算させようってことなのに効率はどうでも良いってなんかちょっと違う気がしますが。。
ループで探索しなくても…
わざわざループで1回ずつ調べなくても、加法定理の倍角の公式で
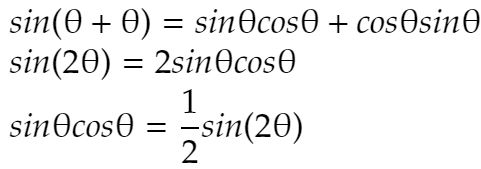
これを代入すれば
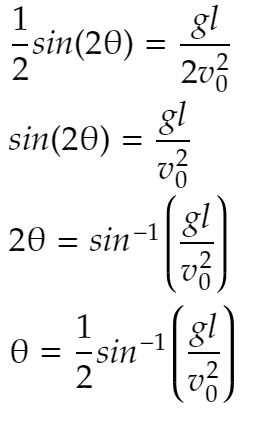
関数電卓にアークサインの機能があれば式を入れるだけでループいらないんですけどね。。。
